最近点对问题

在n(n>=2)个点的集合S中寻找最近点对及最近距离（距离用欧几里得距离度量）。

分治算法求解

  • |S| <= 2：直接计算两点距离
  • |S| == 3：三个点中最近的两点距离
  • |S| > 3：
    • 根据点的x值和y值对S中的点排序
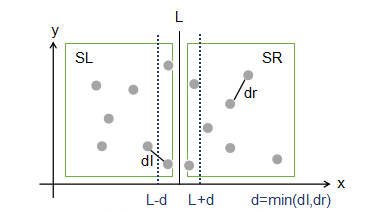
    • 划分集合S为SL和SR，|SL| == |SR|，划分线为L
    • 分别在SL和SR中递归求解子问题，得到两个最小距离dl和dr，令d = min(dl, dr)
    • 将 [L-d, L+d] 内的点以y值排序，对于每一个点(x‘, y’)找出y值在 [y‘-d, y’+d] 内接下来的7个点，计算距离为d’
    • 如果d’ < d，令d = d’，返回d

1
#include <iostream> 
2
#include <ctime>
3
#include <cmath>
4
#include <algorithm>
5
#define NO_DISTANCE 1000000
6
using namespace std; 
7
8
// 二维点Point, x, y范围为[-100, 100]
9
typedef struct Point { float x, y; } Point;
10
11
// 随机初始化points数组中的二维点
12
void InitPoints(Point *points, int length) {
13
    srand(unsigned(time(NULL)));  // 设置随机种子
14
    for(int i=0; i<length; i++) {
15
        points[i].x = (rand()%20000) / 100.0 - 100;    // 调整rand(),使得横纵坐标范围为[-100,100]
16
        points[i].y = (rand()%20000) / 100.0 - 100;
17
    }
18
}
19
20
// 距离公式
21
float Distance(Point a, Point b) {
22
    return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
23
}
24
25
// 排序规则：依照Point中的x 升序
26
bool CmpX(Point a, Point b) {
27
    return a.x < b.x;
28
}
29
30
// 分治策略求最近点对，该两点记为a, b
31
float ClosestPair(Point points[], int length, Point &a, Point &b) {
32
    float distance;        // points中最近两点的距离 
33
    float d1, d2;          // 分割后两子集中各自最小点对的距离
34
    int i=0, j=0, k=0;     // 用于for循环
35
    Point a1, b1, a2, b2;  // 分割后两子集中的最小点对
36
37
    if(length < 2)  return NO_DISTANCE;    // 当子集长度小于2时定义为最大距离：不可达
38
    if(length == 2) {
39
        a = points[0];
40
        b = points[1];
41
        distance = Distance(points[0], points[1]);
42
    }else {
43
        Point *pts1 = new Point[length];     // 开辟两个子集
44
        Point *pts2 = new Point[length];  
45
        sort(points, points+length, CmpX);   // 对points进行排序，排序规则为CmpX
46
        float mid = points[(length-1)/2].x;  // 排完序后的中位数
47
48
        for(i=0; i<length/2; i++) // 左子集
49
            pts1[i] = points[i];
50
        for(int j=0,i=length/2; i<length; i++) // 右子集
51
            pts2[j++] = points[i];
52
53
        d1 = ClosestPair(pts1, length/2, a1, b1);           // 分治求解左子集的最近点对距离
54
        d2 = ClosestPair(pts2, length-length/2, a2, b2);    // 分治求解右子集的最近点对距离
55
        if(d1 < d2) { distance = d1; a = a1; b = b1; }
56
        else { distance = d2; a = a2; b = b2; }
57
58
        // 求解跨分割线并在δ×2δ区间内的最近点对
59
        Point *pts3 = new Point[length];   
60
        for(i=0,k=0; i<length; i++)
61
            if(abs(points[i].x-mid) <= distance)    pts3[k++] = points[i];
62
63
        for(i=0; i<k; i++)
64
            for(j=i+1; j<=i+7&&j<k; j++)    // 只需与有序的邻接的的7个点进行比较
65
                if(Distance(pts3[i], pts3[j]) < distance) { // 跨分割线的两点距离小于已知最小距离
66
                    distance = Distance(pts3[i], pts3[j]);
67
                    a = pts3[i];
68
                    b = pts3[j];
69
                }
70
    }
71
    return distance;
72
}
73
74
// 显示点集
75
void ShowPoints(Point points[], int length) {
76
    for(int i=0; i<length; i++)
77
        cout << "(" << points[i].x << ", " << points[i].y << ")" << endl;
78
}
79
80
int main() {
81
    int N;          // 随机生成的点对个数
82
    Point a, b;     // 最近点对
83
    float diatance; // 最近距离
84
    cout << "请您输入点对个数：";
85
    cin >> N;
86
    if(N < 2)   cout << "点个数要 >= 2 !" << endl;
87
    else {
88
        cout << endl << N << "个随机二维点对：" << endl;
89
        Point *points = new Point[N]; // 点集
90
        InitPoints(points, N);        // 随机初始化点集
91
        ShowPoints(points, N);        // 打印点集
92
        // 求最近点对距离
93
        diatance = ClosestPair(points, N, a, b); 
94
        cout << endl << endl << "按横坐标排序后的点对:" << endl;
95
        ShowPoints(points, N);
96
        cout << endl << "最近点对为：" << "(" << a.x << ", " << a.y << ")和" << "(" << b.x << ", " << b.y << ")" << endl;
97
        cout << "最近点对距离为：" << diatance << endl;
98
    }
99
    return 0;
100
}