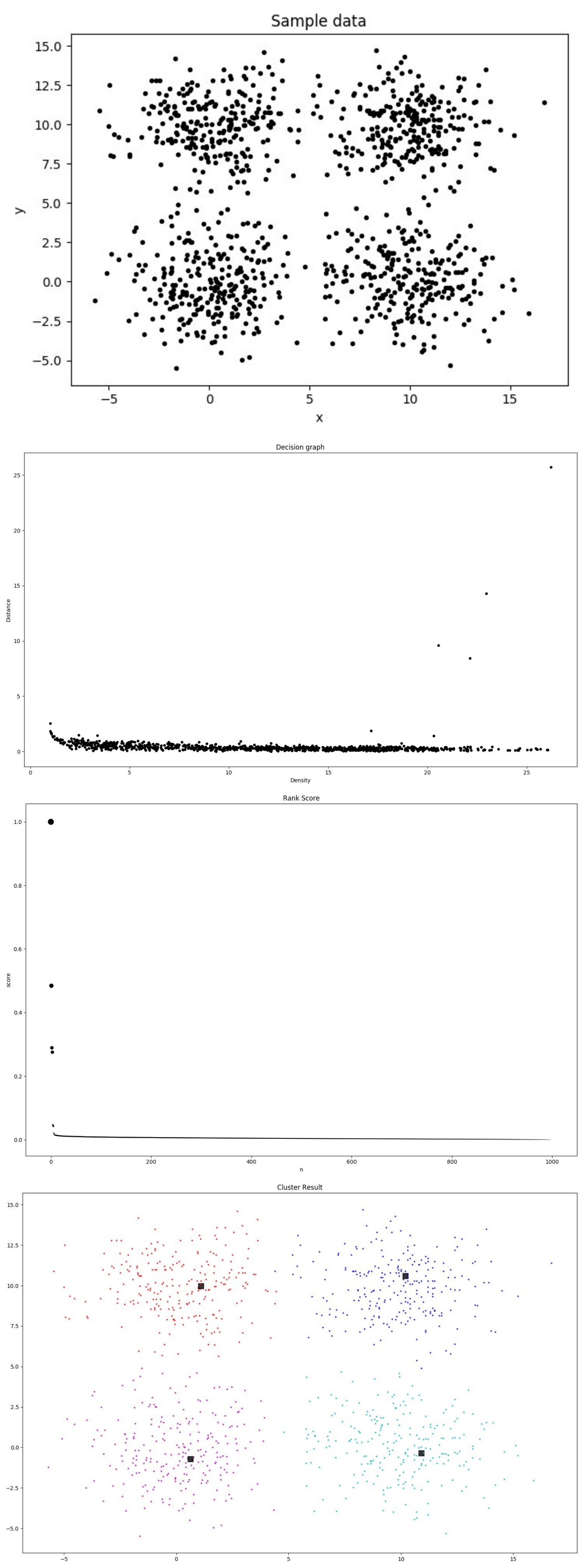
DP聚类算法是Science上一篇文章提出的一种新型的基于密度的聚类算法,思路新颖、方法巧妙。
原文:Clustering by Fast Search and Find of Density Peaks
参考:一种新型聚类算法
基本假设
聚类簇中心被具有较低局部密度的邻居点包围,且与具有更高密度的任何点有相对较大的距离。
算法特点
- 并不局限于球面类别的数据分布,可以对任意形状分布的数据进行聚类
- 相比于DBSCAN算法,DP算法不需要指定密度阈值
相关定义
- 局部密度𝜌i:可通过Cut-off kernel方法或者Gaussian kernel方法计算
- NN距离𝜹i:样本i到任何比其局部密度𝜌i大的样本的距离的最小值
算法描述
- 计算样本集两两之间的距离矩阵
- 计算局部密度列表
- 计算NN距离列表
- 找出聚类中心
- 根据与聚类中心的距离标记其余样本
Python实现
1 | # DP Algorithm |
2 | #!/usr/bin/env python3 |
3 | import numpy as np |
4 | import collections |
5 | import matplotlib.pyplot as plt |
6 | |
7 | |
8 | # 用欧式距离计算样本集的距离矩阵 |
9 | # 参数:样本集x,类型为np.array |
10 | def get_distance(x): |
11 | size = len(x) |
12 | distance = np.zeros(shape=(len(x), len(x))) |
13 | for i in range(0, size - 1): |
14 | for j in range(i + 1, size): |
15 | distance[i][j] = np.sqrt(np.sum(np.power(x[i] - x[j], 2))) |
16 | distance[j][i] = distance[i][j] |
17 | return distance |
18 | |
19 | |
20 | # 选择最优的截断距离dc |
21 | # 参数:距离矩阵distance,平均近邻百分比t(t=2表示平均每个样本的近邻样本数为样本总数的2%) |
22 | def choose_dc(distance, t): |
23 | temp = [] |
24 | for i in range(len(distance[0])): |
25 | for j in range(i + 1, len(distance[0])): |
26 | temp.append(distance[i][j]) |
27 | temp.sort() |
28 | dc = temp[int(len(temp) * t / 100)] |
29 | return dc |
30 | |
31 | |
32 | # 通过Cut-off kernel方法计算局部密度列表 |
33 | # 参数:距离矩阵distance,截断距离dc |
34 | def get_discrete_density(distance, dc): |
35 | density = np.zeros(shape=len(distance)) |
36 | for index, node in enumerate(distance): |
37 | density[index] = len(node[node < dc]) |
38 | return density |
39 | |
40 | |
41 | # 通过Gaussian kernel方法计算局部密度 |
42 | # Gaussian kernel方法:np.sum(np.exp(-(dist / dc) ** 2)) |
43 | # 参数:距离矩阵distance,截断距离dc |
44 | def get_continous_density(distance, dc): |
45 | density = np.zeros(shape=len(distance)) |
46 | for index, dist in enumerate(distance): |
47 | density[index] = np.sum(np.exp(-(dist / dc) ** 2)) |
48 | return density |
49 | |
50 | |
51 | # 计算NN距离列表,找到聚类中心列表 |
52 | # 参数:密度列表density,距离矩阵distance |
53 | def get_dist_center(density, distance): |
54 | dist = np.zeros(shape=len(distance)) # 距离列表 |
55 | closest_leader = np.zeros(shape=len(distance), dtype=np.int32) # 聚类中心列表 |
56 | for index, node in enumerate(distance): |
57 | # 局部密度更大的样本列表 |
58 | larger_density = np.squeeze(np.argwhere(density > density[index])) |
59 | # 如果存在局部密度更大的样本 |
60 | if larger_density.size != 0: |
61 | # 局部密度更大样本与当前样本的距离列表 |
62 | larger_distance = distance[index][larger_density] |
63 | # 当前样本的距离为larger_distance中的最小值 |
64 | dist[index] = np.min(larger_distance) |
65 | # 局部密度更大样本中与当前样本距离相等(最小值可能有多个)的样本集 |
66 | min_distance_sample = np.squeeze(np.argwhere(larger_distance == dist[index])) |
67 | # 有多个局部密度更大且距离当前样本最近的样本时,选择第一个样本作为聚类中心 |
68 | if min_distance_sample.size >= 2: |
69 | min_distance_sample = np.random.choice(a=min_distance_sample) |
70 | if larger_distance.size > 1: |
71 | closest_leader[index] = larger_density[min_distance_sample] |
72 | else: |
73 | closest_leader[index] = larger_density |
74 | # 如果没有局部密度更大的样本(当前样本局部密度最大) |
75 | else: |
76 | dist[index] = np.max(distance) |
77 | closest_leader[index] = index |
78 | return dist, closest_leader |
79 | |
80 | |
81 | # 画原始数据分布图 |
82 | # 参数:样本数据集x |
83 | def draw_x(x): |
84 | for j in range(len(x)): |
85 | plt.scatter(x=x[j, 0], y=x[j, 1], marker='o', c='k', s=8) |
86 | plt.xlabel('x') |
87 | plt.ylabel('y') |
88 | plt.title('Sample data') |
89 | plt.show() |
90 | |
91 | |
92 | # 画密度-距离图 |
93 | # 参数:局部密度列表density,距离列表dist,样本集x |
94 | def draw_density_dist(density, dist, x): |
95 | plt.figure(num=1, figsize=(15, 9)) |
96 | for i in range(len(x)): |
97 | plt.scatter(x=density[i], y=dist[i], c='k', marker='o', s=15) |
98 | plt.xlabel('Density') |
99 | plt.ylabel('Distance') |
100 | plt.title('Decision graph') |
101 | plt.show() |
102 | |
103 | |
104 | # 计算得分:局部密度与距离的乘积,并画出得分排序图 |
105 | # 参数:局部密度列表density,距离列表dist |
106 | def get_score(density, dist): |
107 | # 分别对局部密度和距离做归一化处理 |
108 | normal_density = (density - np.min(density)) / (np.max(density) - np.min(density)) |
109 | normal_distance = (dist - np.min(dist)) / (np.max(dist) - np.min(dist)) |
110 | # 计算得分 |
111 | score = normal_density * normal_distance |
112 | # 画出决策图 |
113 | plt.figure(num=2, figsize=(15, 10)) |
114 | plt.scatter(x=range(len(dist)), y=-np.sort(-score), c='k', marker='o', s=-np.sort(-score) * 100) |
115 | plt.xlabel('n') |
116 | plt.ylabel('score') |
117 | plt.title('Rank Score') |
118 | plt.show() |
119 | return score |
120 | |
121 | |
122 | # 完成聚类 |
123 | # 参数:聚类中心cluster_centers, |
124 | def clustering(cluster_centers, chose_list): |
125 | for i in range(len(cluster_centers)): |
126 | while cluster_centers[i] not in chose_list: |
127 | j = cluster_centers[i] |
128 | cluster_centers[i] = cluster_centers[j] |
129 | C = cluster_centers[:] |
130 | return C # C[i]表示第i点所属最终分类 |
131 | |
132 | |
133 | # 画聚类结果 |
134 | # 参数:聚类簇C,样本集x,聚类中心centers |
135 | def draw_cluster(C, x, centers): |
136 | colors = ['b', 'r', 'c', 'm', 'g', 'y', 'k', 'w', 'gold', 'pink', 'orange', 'purple'] |
137 | center_color = {} |
138 | final = dict(collections.Counter(C)).keys() |
139 | for index, i in enumerate(final): |
140 | center_color[i] = index |
141 | # 画最终聚类图 |
142 | plt.figure(num=3, figsize=(15, 10)) |
143 | for i, categorie in enumerate(C): |
144 | if i in centers: # 标出各个聚类簇的中心 |
145 | plt.scatter(x=x[i, 0], y=x[i, 1], marker='s', s=100, c='K', alpha=0.8) |
146 | else: |
147 | plt.scatter(x=x[i, 0], y=x[i, 1], c=colors[center_color[categorie]], s=5, marker='h', alpha=0.66) |
148 | plt.title('Cluster Result') |
149 | plt.show() |
150 | |
151 | |
152 | # dp聚类算法 |
153 | # 参数:样本数据集X |
154 | def dp(X): |
155 | t = 1.1 # 样本集大小的百分比:1.1% |
156 | distance = get_distance(X) # 样本的距离矩阵 |
157 | dc = choose_dc(distance, t) # 最优截断距离dc(根据t) |
158 | density = get_continous_density(distance, dc) # 局部密度列表 |
159 | dist, cluster_center = get_dist_center(density, distance) # 得到距离列表和聚类中心列表 |
160 | draw_x(X) # 画样本数据分布图 |
161 | draw_density_dist(density, dist, X) # 画密度-距离图 |
162 | scores = get_score(density, dist) # 计算局部密度与距离的乘积,并画出得分排序图 |
163 | cluster_num = int(input('Input clusters num: ')) # 看图决定最终的聚类簇数目 |
164 | centers = np.argsort(-scores)[: cluster_num] # 得分最高的前cluster_num个作为最终聚类中心 |
165 | C = clustering(cluster_center, centers) # 完成所有点的聚类 |
166 | draw_cluster(C, X, centers) # 画出聚类结果图 |
167 | |
168 | |
169 | if __name__ == '__main__': |
170 | data = r'./x_train.txt' |
171 | X = np.loadtxt(data, delimiter=' ', usecols=[0, 1]) |
172 | dp(X) # DP聚类 |
聚类结果