用Dijkstra算法求最短路径

Dijkstra算法是单源最短路算法的一种，可用于求从出发节点到所有可到达节点的最短路长度。

一个例子

有向图 结果

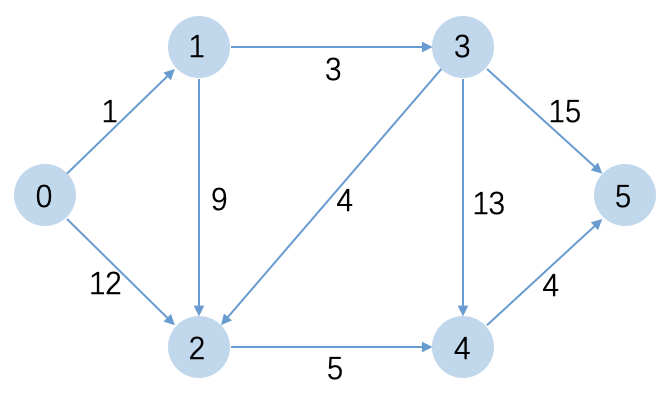程序实现

1
#include <iostream>
2
#include <stack>
3
using namespace std;
4
#define N 100
5
#define INF 100000
6
int E[N][N], dist[N], path[N];  // 边集，与源点的距离，路径
7
8
// dijkstra算法
9
// 参数：源点s，总节点数n
10
void dijkstra(int s, int n){
11
    int visit[N] = {0};  // 已访问节点数组
12
    for(int i=0; i<n; i++)
13
        dist[i] = E[s][i];
14
    visit[s] = 1;
15
    dist[s] = 0;
16
    for(int i=1; i<n; i++){
17
        int min_dsit = INF;  // 最小距离
18
        int min_no;  // 最小距离对应的节点
19
        for(int j=0; j<n; j++)
20
            if(!visit[j] && dist[j] < min_dsit){
21
                min_dsit = dist[j];
22
                min_no = j;
23
            }
24
        visit[min_no] = 1;
25
        for(int j=0; j<n; j++)
26
            if(dist[j] > min_dsit + E[min_no][j]){
27
                path[j] = min_no;  // min_no为到节点j的最后一个中途节点
28
                dist[j] = min_dsit + E[min_no][j];
29
            }            
30
    }
31
}
32
33
// 输出最短路径和距离
34
// 参数：源点s，总节点数n
35
void show(int s, int n){
36
    stack<int> st;
37
    for(int i=1; i<n; i++){
38
        int j = i;
39
        while(path[j] != -1){
40
            st.push(j);
41
            j = path[j];
42
        }
43
        st.push(j);
44
        cout << s << " => " << i << ", distance: " << dist[i] << ", path: " << s;
45
        while(!st.empty()){
46
            cout << "->" << st.top() ;
47
            st.pop();
48
        }
49
        cout << endl;
50
    }
51
}
52
53
int main(){
54
    memset(path, -1, sizeof(path));
55
    int n = 6;
56
    for(int i=0; i<n; i++)
57
        for(int j=0; j<n; j++)
58
            E[i][j] = i==j? 0:INF;
59
    // 有向图举例
60
    E[0][1] = 1;
61
    E[0][2] = 12;
62
    E[1][2] = 9;
63
    E[1][3] = 3;
64
    E[2][4] = 5;
65
    E[3][2] = 4;
66
    E[3][4] = 13;
67
    E[3][5] = 15;
68
    E[4][5] = 4;
69
    // 求源点0到其余节点的最短路径
70
    dijkstra(0, n);
71
    show(0, n);
72
    return 0;
73
}