机器学习相关:最小二乘法拟合曲线。
使用最小二乘法拟和曲线
高斯于1823年在误差e1 ,… , en独立同分布的假定下,证明了最小二乘方法的一个最优性质: 在所有无偏的线性估计类中,最小二乘方法的方差最小!
对于数据(xi, yi) (i = 1, 2, 3…, m),拟合出函数h(x)有误差,即残差:ri = h(xi) - yi,此时L2范数(残差平方和)最小时, h(x) 和 y 相似度最高,更拟合。
一般的H(x)为n次的多项式,H(x) = w0 + w1x + w2x^2 + … wnx^n, w(w0, w1, w2, … , wn)为参数。最小二乘法就是要找到一组 w(w0, w1, w2, … , wn)使得sum((h(xi)-yi)^2) (残差平方和) 最小,即求min(sum((h(xi)-yi)^2))
示例
- 目标函数 y = sin2pix, 加上一个正太分布的噪音干扰,用多项式去拟合
1 | import numpy as np |
2 | from scipy.optimize import leastsq |
3 | import matplotlib.pyplot as plt |
4 | |
5 | # 目标函数 |
6 | def real_func(x): |
7 | return np.sin(2*np.pi*x) |
8 | |
9 | # 生成多项式 |
10 | def fit_func(p, x): |
11 | f = np.poly1d(p) # numpy.poly1d([1,2,3]) 生成 1x^2+2x^1+3x^0 |
12 | return f(x) |
13 | |
14 | # 计算残差 |
15 | def residuals_func(p, x, y): |
16 | ret = fit_func(p, x) - y |
17 | return ret |
18 | |
19 | # 拟合曲线:M为多项式的次数 |
20 | def fitting(M=0): |
21 | # 拟合 |
22 | p_init = np.random.rand(M + 1) # 随机初始化多项式参数 |
23 | p_lsq = leastsq(residuals_func, p_init, args=(x, y)) # 最小二乘法 |
24 | print('Fitting Parameters:', p_lsq[0]) |
25 | # 可视化 |
26 | plt.plot(x_points, real_func(x_points), label='real') |
27 | plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve') |
28 | plt.plot(x, y, 'bo', label='noise') |
29 | plt.legend() |
30 | plt.show() |
31 | return p_lsq |
32 | |
33 | if __name__ == '__main__': |
34 | x = np.linspace(0, 1, 10) |
35 | x_points = np.linspace(0, 1, 1000) |
36 | # 正态分布噪音的目标函数的值y |
37 | y_ = real_func(x) |
38 | y = [np.random.normal(0, 0.1) + y1 for y1 in y_] |
39 | # 0次拟合 |
40 | p_lsq_0 = fitting(M=0) |
- 拟合结果
0次拟合:[0.00461176]
1次拟合:[-1.36961924 0.66545983]
3次拟合:[21.63282404 -31.80863265 10.24969763 0.08377312]
9次拟合:[-1.28594657e+04 5.80684524e+04 -1.09218448e+05 1.10695847e+05 -6.53112529e+04 2.26030006e+04 -4.36787154e+03 3.94053281e+02 -4.24850439e+00 -1.42083411e-01]
| 拟合次数 | 图示 |
|---|---|
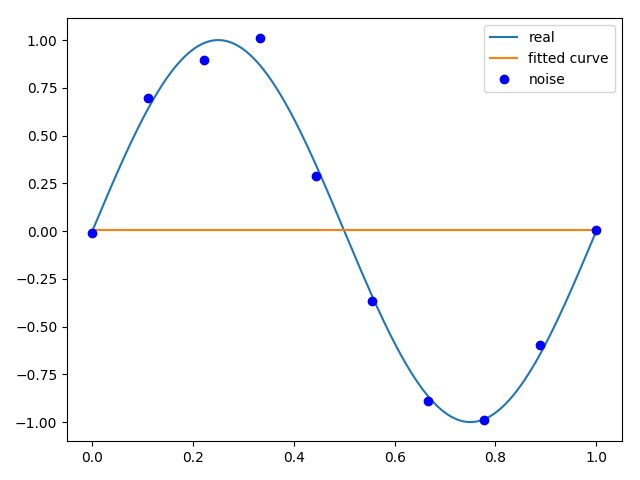 0次拟合 0次拟合 |
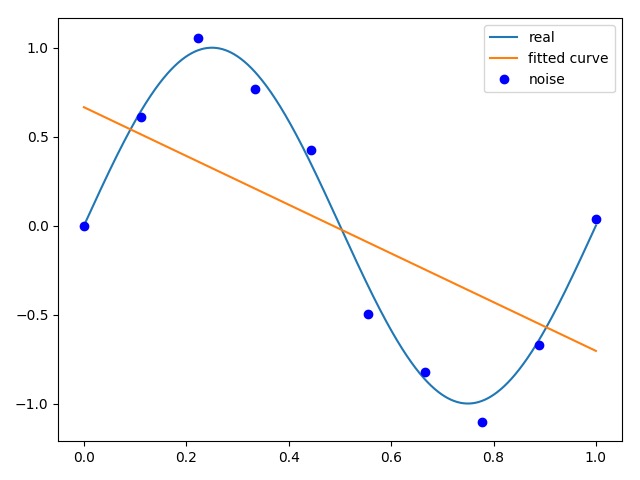 1次拟合 1次拟合 |
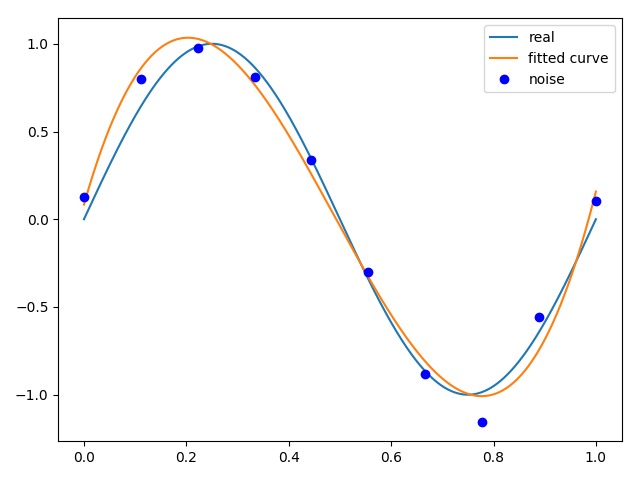 3次拟合 3次拟合 |
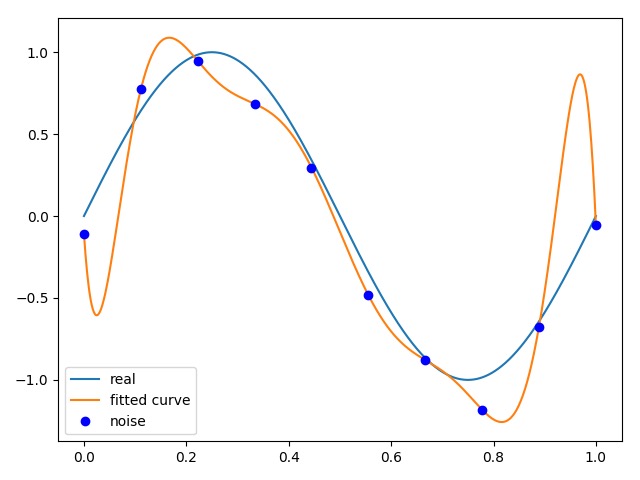 9次拟合 9次拟合 |
当M=9时,多项式曲线通过了每个数据点,但是造成了过拟合。
正则化
结果显示过拟合,我们引入正则化项(regularizer),降低过拟合。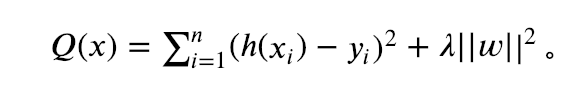
回归问题中,损失函数是平方损失,正则化可以是参数向量的L2范数,也可以是L1范数。
- L1: regularization*abs(p)
- L2: 0.5 * regularization * np.square(p)
1 | # 正则函数 |
2 | regularization = 0.0001 |
3 | def residuals_func_regularization(p, x, y): |
4 | ret = fit_func(p, x) - y |
5 | ret = np.append(ret, np.sqrt(0.5*regularization*np.square(p))) # L2范数作为正则化项 |
6 | return ret |
7 | |
8 | if __name__ == '__main__': |
9 | x = np.linspace(0, 1, 10) |
10 | x_points = np.linspace(0, 1, 1000) |
11 | # 正态分布噪音的目标函数的值y |
12 | y_ = real_func(x) |
13 | y = [np.random.normal(0, 0.1) + y1 for y1 in y_] |
14 | |
15 | # 最小二乘法, 加正则化项 |
16 | p_init = np.random.rand(9 + 1) |
17 | p_lsq_regularization = leastsq(residuals_func_regularization, p_init, args=(x, y)) |
18 | plt.plot(x_points, real_func(x_points), label='real') |
19 | plt.plot(x_points, fit_func(p_lsq_9[0], x_points), label='fitted curve') |
20 | plt.plot(x_points, fit_func(p_lsq_regularization[0], x_points), label='regularization') |
21 | plt.plot(x, y, 'bo', label='noise') |
22 | plt.legend() |
23 | plt.show() |
带有正则化的9次拟合: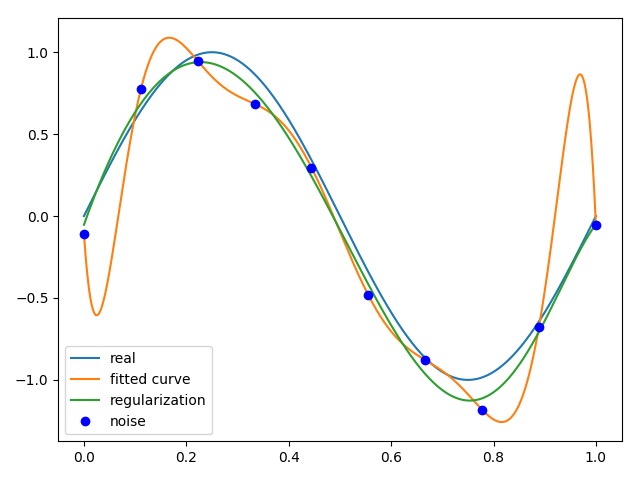
可见,绿色曲线在避免过拟合的影响下,能够最好的完成拟合。
