实现过程中的注意点
适应度计算
在遗传算法中,个体好坏用适应度来衡量,适应度越大说明该个体生存能力越强,也越接近最优解。而TSP问题需要总路径最小,故我们用总路径的倒数来表示个体的适应度。
获取更好的初始化种群
在初始化种群的过程中,对于随机生成的个体,我们随机交换其中的两个城市,如果交换后个体适应度有所提高(该解决方案下TSP路径变短),则更新该个体(发生交换)。
自然选择
自然选择是为了选择一些生存能力较强的个体作为交叉变异的父代,完成种群的繁衍工作。在这个过程中,我们先选取适应度最高的一部分个体作为父代。同时,为避免遗漏一些适应度较低但生存能力较强的个体,我们在剩余个体中,根据其存活率随机选取,并加入到已选择的父代中。
交叉操作
对于一般的编码,交叉操作很简单,按照正常思路做就可以,但是对于TSP问题,我们的个体是城市编号的序列,所以一个个体内部不能有重复编码,而一般的交叉、变异操作很容易导致编码重复。因此我们需要做一定调整:
- 根据交叉点,获取两个父代交叉部分的编码
- 获取两个父代剩余部分编码
- 交叉部分编码完成交换
- 对剩余部分编码去重
- 从交叉部分编码的右边开始以此循环填充剩余部分编码
变异操作
- 依次选取三个点u、v、w,将[v, w]部分编码与[u, v]部分编码交换。
算法流程图
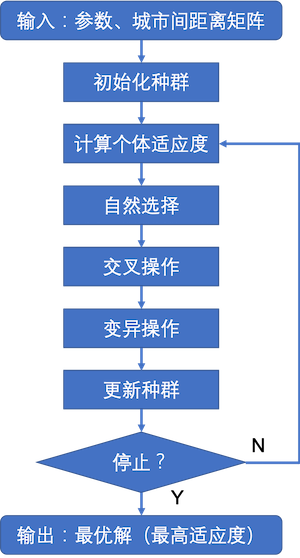
Python实现
1 | """ |
2 | TSP_GA: 遗传算法解决旅行商问题 |
3 | """ |
4 | import random |
5 | import numpy as np |
6 | import matplotlib.pyplot as plt |
7 | |
8 | # 设置参数 |
9 | city_num = 20 # 城市个数 |
10 | epochs = 3000 # 迭代次数 |
11 | population_size = 300 # 种群大小 |
12 | improve_cnt = 1000 # 改良次数 |
13 | mutation_probability = 0.1 # 变异概率 |
14 | retain_rate = 0.3 # 高适应度个体的保留率 |
15 | survival_rate = 0.5 # 低适应度个体的存活率 |
16 | |
17 | print('TSP By GA......') |
18 | print('The number of cities: ', str(city_num)) |
19 | print('The size of population: ', str(population_size)) |
20 | print('The number of generations: ', str(epochs)) |
21 | |
22 | |
23 | # 城市类 |
24 | class City: |
25 | def __init__(self, x, y): |
26 | self.x = x |
27 | self.y = y |
28 | |
29 | |
30 | # 初始化城市 |
31 | def init_cities(): |
32 | cities, x_cities, y_cities = [], [], [] |
33 | for i in range(city_num): |
34 | x, y = random.uniform(0, 10), random.uniform(0, 10) |
35 | cities.append(City(x, y)) |
36 | x_cities.append(x) |
37 | y_cities.append(y) |
38 | return cities |
39 | |
40 | |
41 | # 计算距离 |
42 | def compute_distance(cities): |
43 | distance = np.zeros((len(cities), len(cities))) |
44 | for i in range(len(cities)): |
45 | for j in range(len(cities)): |
46 | if i != j: |
47 | distance[i][j] = ((cities[i].x-cities[j].x)**2 + (cities[i].y-cities[j].y)**2)**0.5 |
48 | return distance |
49 | |
50 | |
51 | # 初始化种群 |
52 | def init_population(distance): |
53 | population = [] |
54 | for i in range(population_size): |
55 | tmp = list(range(city_num)) |
56 | np.random.shuffle(tmp) |
57 | # 改良圈算法求的更好的初始化种群:随机交换两个城市序号,如果总距离减少则更新 |
58 | one_distance = get_all_distance(tmp, distance) |
59 | cnt = improve_cnt # 改良次数 |
60 | for k in range(cnt): |
61 | u = random.randint(0, len(tmp) - 1) |
62 | v = random.randint(0, len(tmp) - 1) |
63 | if u != v: |
64 | new_tmp = tmp.copy() |
65 | new_tmp[u], new_tmp[v] = new_tmp[v], new_tmp[u] |
66 | new_distance = get_all_distance(new_tmp, distance) |
67 | if new_distance < one_distance: |
68 | one_distance = new_distance |
69 | tmp = new_tmp.copy() |
70 | population.append(tmp) |
71 | return population |
72 | |
73 | |
74 | # 计算一个解的总距离 |
75 | def get_all_distance(path, distance): |
76 | one_distance = distance[path[city_num - 1]][path[0]] |
77 | for j in range(city_num - 1): |
78 | one_distance += distance[path[j]][path[j + 1]] |
79 | return one_distance |
80 | |
81 | |
82 | # 计算适应度 |
83 | def get_fitness(population, distance): |
84 | fitness = [] |
85 | for i in population: |
86 | f = 100 / get_all_distance(i, distance) |
87 | fitness.append(f) |
88 | return fitness |
89 | |
90 | |
91 | # 自然选择 |
92 | def selection(population, fitness): |
93 | graded = [[fitness[x], population[x]] for x in range(len(population))] |
94 | graded = [x[1] for x in sorted(graded, reverse=True)] |
95 | retain_length = int(retain_rate * len(graded)) |
96 | parents = graded[:retain_length] |
97 | for i in graded[retain_length:]: |
98 | if random.random() < survival_rate: |
99 | parents.append(i) |
100 | return parents |
101 | |
102 | |
103 | # 交叉操作 |
104 | def crossover(parents): |
105 | children = [] |
106 | while len(children) < population_size - len(parents): |
107 | mail_i = random.randint(0, len(parents) - 1) |
108 | femail_i = random.randint(0, len(parents) - 1) |
109 | if mail_i != femail_i: |
110 | # 交叉父代 |
111 | mail = parents[mail_i] |
112 | femail = parents[femail_i] |
113 | # 交叉点位置 |
114 | left = random.randint(0, len(mail) - 2) |
115 | right = random.randint(left + 1, len(mail) - 1) |
116 | # 两染色体的交叉片段 |
117 | gene1 = mail[left:right] |
118 | gene2 = femail[left:right] |
119 | # 两染色体未交叉片段 |
120 | child1_c = mail[right:] + mail[:right] |
121 | child2_c = femail[right:] + femail[:right] |
122 | child1 = child1_c.copy() |
123 | child2 = child2_c.copy() |
124 | # 去除重复 |
125 | for o in gene2: |
126 | child1_c.remove(o) |
127 | for o in gene1: |
128 | child2_c.remove(o) |
129 | # 完成交叉 |
130 | child1[left:right] = gene2 |
131 | child2[left:right] = gene1 |
132 | child1[right:] = child1_c[0:len(child1) - right] |
133 | child1[:left] = child1_c[len(child1) - right:] |
134 | child2[right:] = child2_c[0:len(child1) - right] |
135 | child2[:left] = child2_c[len(child1) - right:] |
136 | # 更新种群 |
137 | children.append(child1) |
138 | children.append(child2) |
139 | return children |
140 | |
141 | |
142 | # 变异操作 |
143 | def mutation(children): |
144 | for i in range(len(children)): |
145 | if random.random() <= mutation_probability: |
146 | u = random.randint(1, len(children[i]) - 4) |
147 | v = random.randint(u + 1, len(children[i]) - 3) |
148 | w = random.randint(v + 1, len(children[i]) - 2) |
149 | children[i] = children[i][0:u] + children[i][v:w] + children[i][u:v] + children[i][w:] |
150 | |
151 | |
152 | # 初始化:初始化城市、计算距离矩阵、初始化种群 |
153 | cities = init_cities() |
154 | distance = compute_distance(cities) |
155 | # 1.初始化种群 |
156 | population = init_population(distance) |
157 | |
158 | # 遗传算法开始迭代 |
159 | generation = 1 # 当前代 |
160 | print('Start......', end=' ') |
161 | while generation != epochs: |
162 | generation += 1 |
163 | # 2.计算适应度 |
164 | fitness = get_fitness(population, distance) |
165 | # 3.自然选择 |
166 | parents = selection(population, fitness) |
167 | # 4.交叉操作: |
168 | children = crossover(parents) |
169 | # 5.变异操作 |
170 | mutation(children) |
171 | # 6.更新种群 |
172 | population = parents + children |
173 | |
174 | print('Finish.') |
175 | # 获取最优解 |
176 | best_one = np.argmax(fitness) |
177 | best_solution = population[best_one] |
178 | best_distance = get_all_distance(best_solution, distance) |
179 | |
180 | # 获取最优路径 |
181 | best_path = best_solution + [best_solution[0]] |
182 | |
183 | # 输出最优路径 |
184 | print('The best path: ' + str(best_path[0]), end='') |
185 | for i in range(1, len(best_path)): |
186 | print(' ->', str(best_path[i]), end='') |
187 | print() |
188 | # 输出总路径 |
189 | print('The total distance: ', str(best_distance)) |
190 | |
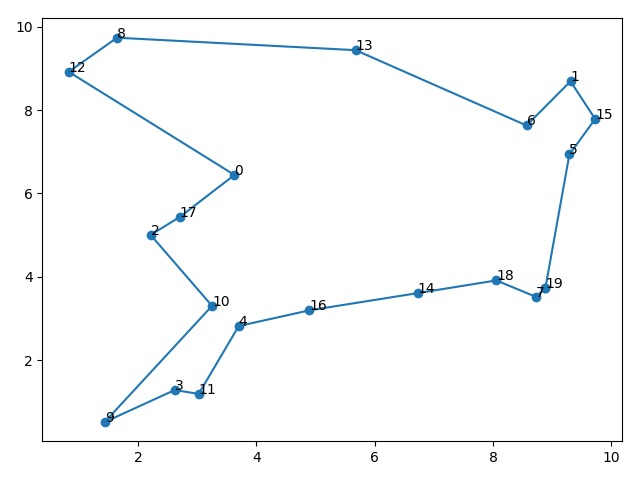
191 | # 画出最优路径 |
192 | X, Y = [], [] |
193 | for i in best_path: |
194 | X.append(cities[i].x) |
195 | Y.append(cities[i].y) |
196 | fig, ax = plt.subplots() |
197 | ax.plot(X, Y, marker='o') |
198 | for i in range(city_num): |
199 | txt = best_path[i] |
200 | ax.annotate(txt, (X[i], Y[i])) |
201 | plt.show() |
运行结果
1 | /usr/local/bin/python3.6 TSP_GA.py |
2 | TSP By GA...... |
3 | The number of cities: 20 |
4 | The size of population: 300 |
5 | The number of generations: 3000 |
6 | Start...... Finish. |
7 | The best path: 19 -> 5 -> 15 -> 1 -> 6 -> 13 -> 8 -> 12 -> 0 -> 17 -> 2 -> 10 -> 9 -> 3 -> 11 -> 4 -> 16 -> 14 -> 18 -> 7 -> 19 |
8 | The total distance: 35.2732056886219 |
9 | |
10 | Process finished with exit code 0 |