特点
- 全局搜索能力
- 多样性保持机制
- 鲁棒性强
- 并行分布式搜索机制
原理
免疫算法是受生物免疫系统的启发而推出的一种新型的智能搜索算法,是一种确定性和随机性选择相结合并具有”勘探”与”开采”能力的启发式随机搜索算法。下表是免疫算法与生物免疫系统概念的对应关系:
| 生物免疫系统 | 免疫算法 |
|---|---|
| 抗原 | 优化问题 |
| 抗体 | 优化问题的可行解 |
| 亲和度 | 可行解的质量 |
| 细胞活化 | 免疫选择 |
| 细胞分化 | 个体克隆 |
| 亲和度成熟 | 变异 |
| 克隆抑制 | 克隆抑制 |
| 动态维持平衡 | 种群刷新 |
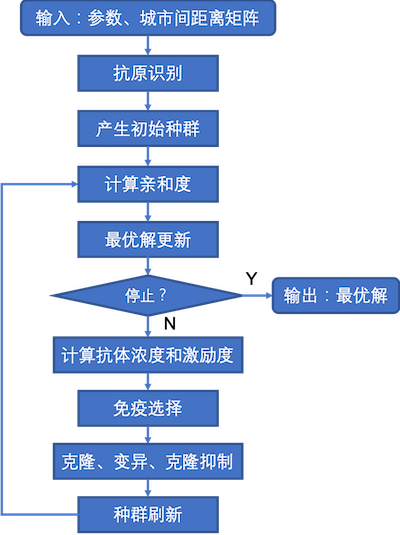
算法流程图
Python实现
1 | """ |
2 | TSP_IA: 免疫算法解决旅行商问题 |
3 | """ |
4 | import numpy as np |
5 | import matplotlib.pyplot as plt |
6 | |
7 | # 设置参数 |
8 | city_num = 20 # 城市数目 |
9 | population_size = 100 # 免疫个体数目 |
10 | epochs = 500 # 最大免疫代数 |
11 | clone_number = 10 # 克隆数目 |
12 | |
13 | print('TSP By IA......') |
14 | print('The number of cities: ', str(city_num)) |
15 | print('The number of immune individuals: ', str(population_size)) |
16 | print('The number of immune generations: ', str(epochs)) |
17 | |
18 | |
19 | # 初始化变异个体 |
20 | def init_population(city_num, population_size): |
21 | individuals = np.zeros((city_num, population_size)) |
22 | for i in range(population_size): |
23 | individuals[:, i] = np.random.permutation(range(0, city_num)) |
24 | return individuals.astype(int) |
25 | |
26 | |
27 | # 计算城市两两间的距离矩阵 |
28 | def compute_distance(city_size, cities_location): |
29 | dismat = np.zeros((city_size, city_size)) |
30 | for i in range(city_size): |
31 | for j in range(i, city_size): |
32 | dismat[i][j] = dismat[j][i] = np.linalg.norm(cities_location[i] - cities_location[j]) |
33 | return dismat |
34 | |
35 | |
36 | # 计算一个解的总距离 |
37 | def get_all_distance(path, distance): |
38 | one_distance = distance[path[city_num - 1]][path[0]] |
39 | for j in range(city_num - 1): |
40 | one_distance += distance[path[j]][path[j + 1]] |
41 | return one_distance |
42 | |
43 | |
44 | # 初始化城市坐标:横纵坐标的取值范围都是0~10 |
45 | cities_location = np.random.uniform(0, 10, (city_num, 2)) |
46 | # 计算城市间的距离矩阵 |
47 | distance = compute_distance(city_num, cities_location) |
48 | # 初始化免疫个体种群 |
49 | population = init_population(city_num, population_size) |
50 | # 计算每个免疫个体的路径总长度 |
51 | individual_lengths = np.zeros((population_size, 1)) |
52 | for i in range(population_size): |
53 | individual_lengths[i] = get_all_distance(population[:, i], distance) |
54 | |
55 | # 根据路径总长度升序排序 |
56 | sorted_indexs = np.argsort(individual_lengths, axis=0) # 升序排序索引 |
57 | sorted_population = np.zeros((city_num, population_size)) # 升序排序的免疫种群 |
58 | sorted_individual_lengths = np.zeros((population_size, 1)) # 升序排序的免疫个体路径长度 |
59 | for i in range(population_size): |
60 | sorted_population[:, i] = population[:, sorted_indexs[i][0]] |
61 | sorted_individual_lengths[i, 0] = individual_lengths[sorted_indexs[i][0], 0] |
62 | |
63 | # 记录每一代的最短路径 |
64 | record_min_length = np.zeros((epochs, 1)) |
65 | # 开始迭代 |
66 | print('Start......', end=' ') |
67 | for gen in range(epochs): |
68 | # 免疫种群(总种群的一半) |
69 | half_of_all = np.zeros((city_num, int(population_size / 2)), dtype=int) |
70 | half_of_all_length = np.zeros((int(population_size / 2), 1)) |
71 | for i in range(int(population_size / 2)): |
72 | # 选择操作 |
73 | tile_i_th = np.tile(sorted_population[:, i], (clone_number, 1)) |
74 | clone_individuals = np.transpose(tile_i_th) |
75 | for j in range(clone_number): |
76 | p1, p2 = np.random.randint(0, city_num, size=2) |
77 | clone_individuals[p1, j], clone_individuals[p2, j] = clone_individuals[p2, j], clone_individuals[p1, j] |
78 | clone_individuals[:, 0] = sorted_population[:, i] |
79 | # 克隆抑制 |
80 | clone_individuals = clone_individuals.astype(int) |
81 | clone_individuals_lengths = np.zeros((clone_number, 1)) |
82 | for j in range(clone_number): |
83 | clone_individuals_lengths[j, 0] = get_all_distance(clone_individuals[:, j], distance) |
84 | sorted_indexs = np.argsort(clone_individuals_lengths, axis=0) |
85 | sorted_clone_individuals = np.zeros((city_num, clone_number)) |
86 | sorted_clone_individuals_lengths = np.zeros((clone_number, 1)) |
87 | for k in range(clone_number): |
88 | sorted_clone_individuals[:, k] = clone_individuals[:, sorted_indexs[k][0]] |
89 | sorted_clone_individuals_lengths[k, 0] = clone_individuals_lengths[sorted_indexs[k][0], 0] |
90 | half_of_all[:, i] = sorted_clone_individuals[:, 0] |
91 | half_of_all_length[i, 0] = sorted_clone_individuals_lengths[0, 0] |
92 | # 种群刷新 |
93 | # 初始化新种群(另一半) |
94 | new_half_of_all = np.zeros((city_num, int(population_size / 2)), dtype=int) |
95 | new_half_of_all_length = np.zeros((int(population_size / 2), 1)) |
96 | for i in range(int(population_size / 2)): |
97 | init_one = init_population(city_num, 1) |
98 | init_one.shape = city_num |
99 | new_half_of_all[:, i] = init_one |
100 | new_half_of_all_length[i, 0] = get_all_distance(new_half_of_all[:, i], distance) |
101 | # 免疫种群和新种群合并 |
102 | updated_population = np.append(half_of_all, new_half_of_all, axis=1) |
103 | updated_population_length = np.append(half_of_all_length, new_half_of_all_length, axis=0) |
104 | # 根据总路径长度升序排序免疫种群 |
105 | sorted_indexs = np.argsort(updated_population_length, axis=0) |
106 | sorted_population = np.zeros((city_num, population_size)) |
107 | sorted_individual_lengths = np.zeros((population_size, 1)) |
108 | for i in range(population_size): |
109 | sorted_population[:, i] = updated_population[:, sorted_indexs[i][0]] |
110 | sorted_individual_lengths[i, 0] = updated_population_length[sorted_indexs[i][0], 0] |
111 | # 记录最小路径长度 |
112 | record_min_length[gen, 0] = sorted_individual_lengths[0, 0] |
113 | |
114 | print('Finish.') |
115 | # 获取最优个体(最优路径)、最优路径长度 |
116 | best_solution = list(map(int, sorted_population[:, 0].astype(int))) |
117 | best_path = best_solution + [best_solution[0]] |
118 | best_length = record_min_length[-1, 0] |
119 | |
120 | # 输出最优路径 |
121 | print('The best path: ' + str(best_path[0]), end='') |
122 | for i in range(1, len(best_path)): |
123 | print(' ->', str(best_path[i]), end='') |
124 | print() |
125 | # 输出总路径 |
126 | print('The total distance: ', str(best_length)) |
127 | |
128 | # 画出最优路径 |
129 | X, Y = [], [] |
130 | for i in best_path: |
131 | X.append(cities_location[i, 0]) |
132 | Y.append(cities_location[i, 1]) |
133 | fig, ax = plt.subplots() |
134 | ax.plot(X, Y, marker='o') |
135 | for i in range(city_num): |
136 | txt = best_path[i] |
137 | ax.annotate(txt, (X[i], Y[i])) |
138 | plt.show() |
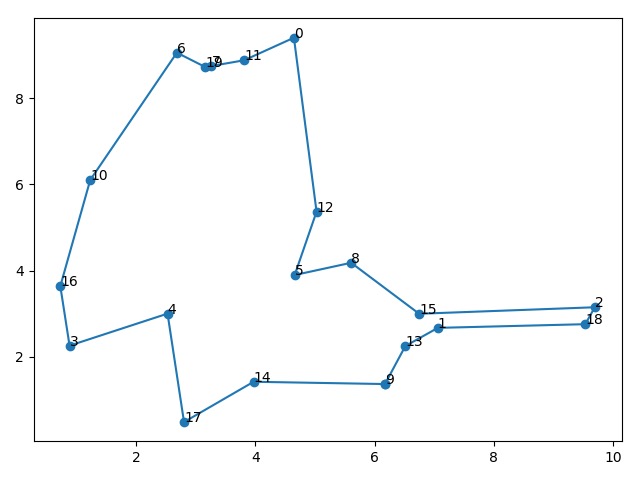
运行结果
1 | /usr/local/bin/python3.6 TSP_IA.py |
2 | TSP By IA...... |
3 | The number of cities: 20 |
4 | The number of immune individuals: 100 |
5 | The number of immune generations: 500 |
6 | Start...... Finish. |
7 | The best path: 9 -> 13 -> 1 -> 18 -> 2 -> 15 -> 8 -> 5 -> 12 -> 0 -> 11 -> 7 -> 19 -> 6 -> 10 -> 16 -> 3 -> 4 -> 17 -> 14 -> 9 |
8 | The total distance: 33.18839279827168 |
9 | |
10 | Process finished with exit code 0 |