蚁群算法解决旅行商问题

什么是旅行商问题（TSP）？什么是蚁群算法？

基本原理

  • 蚂蚁在路径上释放信息素。
  • 碰到还没走过的路口，就随机挑选一条路走。同时，释放与路径长度有关的信息素。
  • 信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高路径。
  • 最优路径上的信息素浓度越来越大。
  • 最终蚁群找到最优寻食路径。

人工蚁群与真实蚁群对比

  • 相同点：
    • 都存在个体相互交流的通信机制
    • 都要完成寻找最短路径的任务
    • 都采用根据当前信息进行路径选择的随机选择策略
  • 不同点：
    • 人工蚂蚁具有记忆能力
    • 人工蚂蚁选择路径时不是完全盲目的
    • 人工蚂蚁生活在离散时间环境中

蚂蚁

  • 每次周游，每只蚂蚁在其经过的支路（i,j）上都留下信息素。
  • 蚂蚁选择城市的概率与城市之间的距离和当前连接支路上所包含的信息素余量有关。

主要参数

  • Alpha：信息启发式，Alpha值越大，蚂蚁选择之前走过路径的可能性就越大；值越小，蚁群搜索范围就越小，容易陷入局部最优。
  • Beta：期望启发式因子，Beta越大，蚁群越容易选择局部较短路径，这时算法收敛速度加快，但随机性不高，容易得到局部最优解。
  • M：蚁群数量，M越大，最优解越精确，但会产生重复解，消耗资源，增大时间复杂度。
  • RHO：信息发挥因子，1-RHO表示残留因子，RHO过小，各路径上残留信息素过多，导致无效路径继续被搜素，影响算法收敛效率；RHO过大，有效路径可能会被放弃搜索，影响最优解的搜索。
  • Q：用于信息素增量的设置，在蚁周模型下，信息素增量=Q/当前解路径总长度。蚁周模型利用的是全局信息，即蚂蚁完成一个循环后更新所有路径上的信息素。

蚁群算法中参数的理想设置

参数 取值范围
Alpha [0, 5]
Beta [0, 5]
Q [10, 10000]
RHO [0.1, 0.99]

算法流程图

Python实现

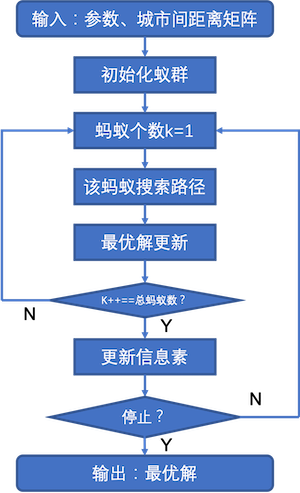
1
"""
2
TSP_ACO: 蚁群算法解决旅行商问题
3
"""
4
import random
5
import copy
6
import matplotlib.pyplot as plt
7
8
# 设置参数
9
epochs = 300  # 最大代数
10
ALPHA = 1  # 信息启发因子(值越大，蚂蚁选择之前走过路径的可能性就越大；值越小，蚁群搜索范围就越小，容易陷入局部最优)
11
BETA = 2  # Beta越大，蚁群越容易选择局部较短路径，这时算法收敛速度加快，但随机性不高，容易得到局部最优解
12
RHO = 0.5
13
Q = 100.0
14
# 城市数，蚁群
15
city_num = 20
16
ant_num = city_num
17
location_x = [
18
    178, 272, 176, 171, 650, 499, 267, 703, 408, 437,
19
    428, 614, 36, 360, 482, 666, 597, 209, 201, 492]
20
location_y = [
21
    170, 395, 198, 151, 242, 556, 57, 401, 305, 421,
22
    490, 213, 524, 244, 114, 104, 552, 70, 425, 227]
23
24
# 城市距离和信息素
25
distance_graph = [[0.0 for col in range(city_num)] for raw in range(city_num)]
26
pheromone_graph = [[1.0 for col in range(city_num)] for raw in range(city_num)]
27
28
print('TSP By ACO......')
29
print('The number of cities: ', str(city_num))
30
31
32
# 蚂蚁类
33
class Ant(object):
34
    # 初始化
35
    def __init__(self, ID):
36
        self.ID = ID  # ID
37
        self.__clean_data()  # 随机初始化出生点
38
39
    # 初始数据
40
    def __clean_data(self):
41
        self.path = []  # 当前蚂蚁的路径
42
        self.total_distance = 0.0  # 当前路径的总距离
43
        self.move_count = 0  # 移动次数
44
        self.current_city = -1  # 当前停留的城市
45
        self.open_table_city = [True for i in range(city_num)]  # 探索城市的状态
46
        city_index = random.randint(0, city_num - 1)  # 随机初始出生点
47
        self.current_city = city_index
48
        self.path.append(city_index)
49
        self.open_table_city[city_index] = False
50
        self.move_count = 1
51
52
    # 选择下一个城市
53
    def __choice_next_city(self):
54
        next_city = -1
55
        select_citys_prob = [0.0 for i in range(city_num)]  # 存储去下个城市的概率
56
        total_prob = 0.0
57
        # 获取去下一个城市的概率
58
        for i in range(city_num):
59
            if self.open_table_city[i]:
60
                # 计算概率：与信息素浓度成正比，与距离成反比
61
                select_citys_prob[i] = pow(pheromone_graph[self.current_city][i], ALPHA) * pow(
62
                    (1.0 / distance_graph[self.current_city][i]), BETA)
63
                total_prob += select_citys_prob[i]
64
65
        # 轮盘选择城市
66
        if total_prob > 0.0:
67
            # 产生一个随机概率, 0.0～total_prob
68
            temp_prob = random.uniform(0.0, total_prob)
69
            for i in range(city_num):
70
                if self.open_table_city[i]:
71
                    # 轮次相减
72
                    temp_prob -= select_citys_prob[i]
73
                    if temp_prob < 0.0:
74
                        next_city = i
75
                        break
76
77
        if next_city == -1:
78
            next_city = random.randint(0, city_num - 1)
79
            while self.open_table_city[next_city] is False:  # if==False,说明已经遍历过了
80
                next_city = random.randint(0, city_num - 1)
81
82
        # 返回下一个城市序号
83
        return next_city
84
85
    # 计算路径总距离
86
    def __cal_total_distance(self):
87
        temp_distance = 0.0
88
        for i in range(1, city_num):
89
            start, end = self.path[i], self.path[i - 1]
90
            temp_distance += distance_graph[start][end]
91
        # 回路
92
        end = self.path[0]
93
        temp_distance += distance_graph[start][end]
94
        self.total_distance = temp_distance
95
96
    # 移动操作
97
    def __move(self, next_city):
98
        self.path.append(next_city)
99
        self.open_table_city[next_city] = False
100
        self.total_distance += distance_graph[self.current_city][next_city]
101
        self.current_city = next_city
102
        self.move_count += 1
103
104
    # 搜索路径
105
    def search_path(self):
106
        # 初始化数据
107
        self.__clean_data()
108
109
        # 搜素路径，遍历完所有城市为止
110
        while self.move_count < city_num:
111
            # 移动到下一个城市
112
            next_city = self.__choice_next_city()
113
            self.__move(next_city)
114
115
        # 计算路径总长度
116
        self.__cal_total_distance()
117
118
119
# TSP问题
120
class TSP:
121
    def __init__(self):
122
        self.ants = [Ant(ID) for ID in range(ant_num)]  # 初始蚁群
123
        self.best_ant = Ant(-1)  # 初始最优解
124
        self.best_ant.total_distance = 1 << 31  # 初始最大距离
125
        self.iter = 1  # 初始化迭代次数
126
        # 初始城市之间的信息素
127
        for i in range(city_num):
128
            for j in range(city_num):
129
                pheromone_graph[i][j] = 1.0
130
        # 计算城市之间的距离
131
        for i in range(city_num):
132
            for j in range(city_num):
133
                temp_distance = pow((location_x[i] - location_x[j]), 2) + pow((location_y[i] - location_y[j]), 2)
134
                temp_distance = pow(temp_distance, 0.5)
135
                distance_graph[i][j] = float(int(temp_distance + 0.5))
136
137
    # 更新信息素
138
    def __update_pheromone_gragh(self):
139
        # 获取每只蚂蚁在其路径上留下的信息素
140
        temp_pheromone = [[0.0 for col in range(city_num)] for raw in range(city_num)]
141
        for ant in self.ants:
142
            for i in range(1, city_num):
143
                start, end = ant.path[i - 1], ant.path[i]
144
                # 在路径上的每两个相邻城市间留下信息素，与路径总距离反比
145
                temp_pheromone[start][end] += Q / ant.total_distance
146
                temp_pheromone[end][start] = temp_pheromone[start][end]
147
148
        # 更新所有城市之间的信息素，旧信息素衰减加上新迭代信息素
149
        for i in range(city_num):
150
            for j in range(city_num):
151
                pheromone_graph[i][j] = pheromone_graph[i][j] * RHO + temp_pheromone[i][j]
152
153
    # 开始搜索
154
    def search_path(self):
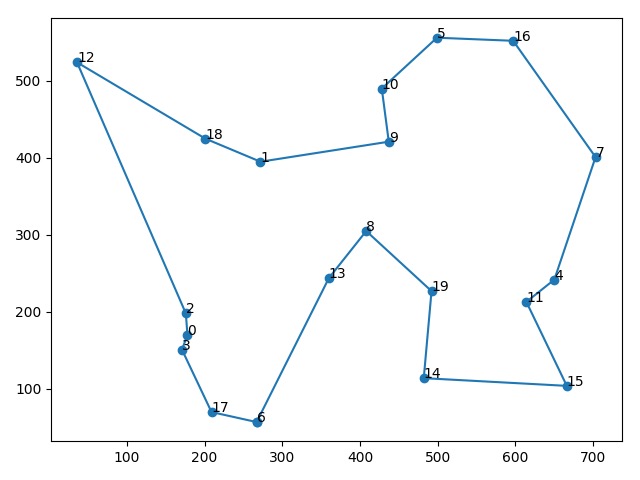
155
        while self.iter < epochs:
156
            # 遍历每一只蚂蚁
157
            for ant in self.ants:
158
                # 搜索一条路径
159
                ant.search_path()
160
                # 与当前最优蚂蚁比较
161
                if ant.total_distance < self.best_ant.total_distance:
162
                    # 更新最优解
163
                    self.best_ant = copy.deepcopy(ant)
164
            # 更新信息素
165
            self.__update_pheromone_gragh()
166
            # print(u"迭代次数：", self.iter, u"最佳路径总距离：", int(self.best_ant.total_distance))
167
            self.iter += 1
168
        return self.best_ant.path, self.best_ant.total_distance
169
170
171
if __name__ == '__main__':
172
    print('Start......', end=' ')
173
    # 获取最优个体（最优路径）、最优路径长度
174
    best_solution, best_length = TSP().search_path()
175
    print('Finish.')
176
    best_path = best_solution + [best_solution[0]]
177
178
    # 输出最优路径
179
    print('The best path: ' + str(best_path[0]), end='')
180
    for i in range(1, len(best_path)):
181
        print(' ->', str(best_path[i]), end='')
182
    print()
183
    # 输出总路径
184
    print('The total distance: ', str(best_length))
185
186
    # 画出最优路径
187
    X, Y = [], []
188
    for i in best_path:
189
        X.append(location_x[i])
190
        Y.append(location_y[i])
191
    fig, ax = plt.subplots()
192
    ax.plot(X, Y, marker='o')
193
    for i in range(city_num):
194
        txt = best_path[i]
195
        ax.annotate(txt, (X[i], Y[i]))
196
    plt.show()

运行结果

1
/usr/local/bin/python3.6 TSP_ACO.py
2
TSP By ACO......
3
The number of cities:  20
4
Start...... Finish.
5
The best path: 6 -> 17 -> 3 -> 0 -> 2 -> 12 -> 18 -> 1 -> 9 -> 10 -> 5 -> 16 -> 7 -> 4 -> 11 -> 15 -> 14 -> 19 -> 8 -> 13 -> 6
6
The total distance:  2470.0
7
8
Process finished with exit code 0