排序算法汇总。动画演示:一份清晰又全面的排序算法攻略
- 内排序
- 外排序
稳定性:相同的元素在排序前和排序后的前后位置是否发生改变,没有改变则排序是稳定的,改变则排序是不稳定的 ——八大排序算法的稳定性
1.插入排序
逐个处理待排序的记录,每个记录与前面已排序已排序的子序列进行比较,将它插入子序列中正确位置
代码
1 | template<class Elem> |
2 | void inssort(Elem A[], int n) |
3 | { |
4 | for(int i=1; i<n; i++) |
5 | for(int j=i; j>=1 && A[j]<A[j-1]; j--) |
6 | swap(A, j, j-1); |
7 | } |
性能
- 最佳:升序。时间复杂度为O(n)
- 最差:降序。时间复杂度为O(n^2)
- 平均:对于每个元素,前面有一半元素比它大。时间复杂度为O(n^2)
- 辅助空间:O(1)
- 稳定性:稳定
如果待排序数据已经“基本有序”,使用插入排序可以获得接近O(n)的性能
优化
1 | template<class Elem> |
2 | void inssort(Elem A[], int n) |
3 | { |
4 | for(int i=1; i<n; i++){ |
5 | int j = i; |
6 | int tp = A[j]; |
7 | for(; j>=1 && tp<A[j-1]; j--) |
8 | A[j] = A[j - 1]; |
9 | A[j] = tp; |
10 | } |
11 | } |
2.二分插入排序
代码
1 | template<class Elem> |
2 | void InsertionSortDichotomy(Elem A[], int n) |
3 | { |
4 | for (int i=1; i<n; i++) |
5 | { |
6 | int get = A[i]; // 右手抓到一张扑克牌 |
7 | int left = 0; // 拿在左手上的牌总是排序好的,所以可以用二分法 |
8 | int right = i - 1; // 手牌左右边界进行初始化 |
9 | while(left <= right) // 采用二分法定位新牌的位置 |
10 | { |
11 | int mid = (left + right) / 2; |
12 | if (A[mid] > get) |
13 | right = mid - 1; |
14 | else |
15 | left = mid + 1; |
16 | } |
17 | for(int j=i-1; j>=left; j--) // 将欲插入新牌位置右边的牌整体向右移动一个单位 |
18 | A[j+1] = A[j]; |
19 | A[left] = get; // 将抓到的牌插入手牌 |
20 | } |
21 | } |
性能
- 最佳:时间复杂度为O(nlogn)
- 最差:时间复杂度为O(n^2)
- 平均:时间复杂度为O(n^2)
- 辅助空间:O(1)
- 稳定性:稳定
3.冒泡排序
从数组的底部比较到顶部,比较相邻元素。如果下面的元素更小则交换,否则,上面的元素继续往上比较。这个过程每次使最小元素像个“气泡”似地被推到数组的顶部
代码
1 | template<class Elem> |
2 | void bubsort(Elem A[], int n) |
3 | { |
4 | for(int i=0; i<n-1; i++) |
5 | for(int j=n-1; j>i; j--) |
6 | if(A[j] < A[j-1]) |
7 | swap(A, j, j-1); |
8 | } |
性能
- 最佳:时间复杂度为O(n)
- 最差:时间复杂度为O(n^2)
- 平均:时间复杂度为O(n^2)
- 辅助空间:O(1)
- 稳定性:稳定
优化
增加一个变量flag,用于记录一次循环是否发生了交换,如果没发生交换说明已经有序,可以提前结束
1 | template<class Elem> |
2 | void bubsort(Elem A[], int n) |
3 | { |
4 | bool flag; |
5 | for(int i=0; i<n-1; i++) |
6 | { |
7 | flag = false; // 一趟前flag置为假 |
8 | for(int j=n-1; j>i; j--) |
9 | if(A[j] < A[j-1]) |
10 | { |
11 | swap(A, j, j-1); |
12 | flag = true; // 一旦有交换,flag置为真 |
13 | } |
14 | if(!flag) // 本趟没有发生交换,中途结束算法 |
15 | return; |
16 | } |
17 | } |
4.鸡尾酒排序(冒泡排序的改进)
代码
1 | template<class Elem> |
2 | void CocktailSort(Elem a[], int n) |
3 | { |
4 | int left = 0; // 初始化边界 |
5 | int right = n - 1; |
6 | while(left < right) |
7 | { |
8 | for(int i=left; i<right; i++) // 前半轮,将最大元素放到后面 |
9 | if(a[i] > a[i+1]) |
10 | swap(a[i], a[i+1]); |
11 | right--; |
12 | for(int i=right; i>left; i--) // 后半轮,将最小元素放到前面 |
13 | if(a[i-1] > a[i]) |
14 | swap(a[i-1], a[i]); |
15 | left++; |
16 | } |
17 | } |
性能
- 最佳:时间复杂度为O(n)
- 最差:时间复杂度为O(n^2)
- 平均:时间复杂度为O(n^2)
- 辅助空间:O(1)
- 稳定性:稳定
5.选择排序
第i次“选择”数组中第i小的记录,并将该记录放到数组的第i个位置。换句话说,每次从未排序的序列中找到最小元素,放到未排序数组的最前面
代码
1 | template<class Elem> |
2 | void selsort(Elem A[], int n) |
3 | { |
4 | for(int i=0; i<n-1; i++){ |
5 | int lowindex = i; |
6 | for(int j=i+1; j<n; j++) |
7 | if(A[j] < A[lowindex]) |
8 | lowindex = j; |
9 | swap(A, i, lowindex); // n次交换 |
10 | } |
11 | } |
性能
不管数组是否有序,在从未排序的序列中查找最小元素时,都需要遍历完最小序列,所以时间复杂度为O(n^2)
- 最佳:时间复杂度为O(n^2)
- 最差:时间复杂度为O(n^2)
- 平均:时间复杂度为O(n^2)
- 辅助空间:O(1)
- 稳定性:不稳定
优化
每次内层除了找出一个最小值,同时找出一个最大值(初始为数组结尾)。将最小值与每次处理的初始位置的元素交换,将最大值与每次处理的末尾位置的元素交换。这样一次循环可以将数组规模减小2,相比于原有的方案(减小1)会更快
6.希尔排序
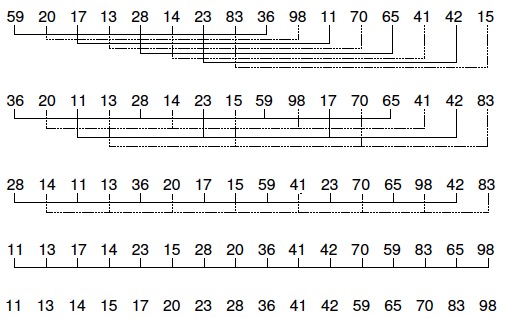
shell排序在不相邻的元素之间比较和交换。利用了插入排序的最佳时间代价特性,它试图将待排序序列变成基本有序的,然后再用插入排序来完成排序工作
在执行每一次循环时,Shell排序把序列分为互不相连的子序列,并使各个子序列中的元素在整个数组中的间距相同,每个子序列用插入排序进行排序。每次循环增量是前一次循环的1/2,子序列元素是前一次循环的2倍
最后一轮将是一次“正常的”插入排序(即对包含所有元素的序列进行插入排序)
代码
1 | const int INCRGAP = 3; |
2 | |
3 | template<class Elem> |
4 | void shellsort(Elem A[], int n) |
5 | { |
6 | for(int incr=n/INCRGAP; incr>0; incr/=INCRGAP) // 遍历所有增量大小 |
7 | { |
8 | for(int i=0; i<incr; i++) |
9 | { |
10 | // 对子序列进行插入排序,当增量为1时,对所有元素进行最后一次插入排序 |
11 | for(int j=i+incr; j<n; j+=incr) |
12 | { |
13 | for(int k=j; k>i&&A[k]<A[k-incr]; k-=incr) |
14 | { |
15 | swap(A, k, k-incr); |
16 | } |
17 | } |
18 | } |
19 | } |
20 | } |
性能
选择适当的增量序列可使Shell排序比其他排序法更有效,一般来说,增量每次除以2时并没有多大效果,而“增量每次除以3”时效果更好
当选择“增量每次除以3”递减时,Shell排序的平均运行时间是O(n^(1.5))
- 最佳:根据步长序列的不同而不同
- 最差:根据步长序列的不同而不同,已知最好的为O(n(logn)^2)
- 平均:时间复杂度为O(n)
- 辅助空间:O(1)
- 稳定性:不稳定
7.快速排序
首先选择一个轴值,小于轴值的元素被放在数组中轴值左侧,大于轴值的元素被放在数组中轴值右侧,这称为数组的一个分割(partition)。快速排序再对轴值左右子数组分别进行类似的操作
选择轴值有多种方法。最简单的方法是使用首或尾元素。但是,如果输入的数组是正序或者逆序时,会将所有元素分到轴值的一边。较好的方法是随机选取轴值
代码
1 | template <class Elem> |
2 | int partition(Elem A[], int i, int j) |
3 | { |
4 | // 这里选择尾元素作为轴值,轴值的选择可以设计为一个函数 |
5 | // 如果选择的轴值不是尾元素,还需将轴值与尾元素交换 |
6 | int pivot = A[j]; |
7 | int l = i - 1; |
8 | for(int r=i; r<j; r++) |
9 | if(A[r] <= pivot) |
10 | swap(A, ++l, r); |
11 | swap(A, ++l, j); // 将轴值从末尾与++l位置的元素交换 |
12 | return l; |
13 | } |
14 | template <class Elem> |
15 | void qsort(Elem A[], int i, int j) |
16 | { |
17 | if(j <= i) return; |
18 | int p = partition<Elem>(A, i, j); |
19 | qsort<Elem>(A, i, p - 1); |
20 | qsort<Elem>(A, p+1, j); |
21 | } |
性能
- 最佳:时间复杂度为O(nlogn)
- 最差:每次处理将所有元素划分到轴值一侧,时间复杂度为O(n^2)
- 平均:时间复杂度为O(nlogn)
- 辅助空间:O(logn)
- 稳定性:不稳定
快速排序平均情况下运行时间与其最佳情况下的运行时间很接近,而不是接近其最坏情况下的运行时间。快速排序是所有内部排序算法中平均性能最优的排序算法
优化
最明显的改进之处是轴值的选取,如果轴值选取合适,每次处理可以将元素较均匀的划分到轴值两侧:三者取中法:三个随机值的中间一个。为了减少随机数生成器产生的延迟,可以选取首中尾三个元素作为随机值
当n很小时,快速排序会很慢。因此当子数组小于某个长度(经验值:9)时,什么也不要做。此时数组已经基本有序,最后调用一次插入排序完成最后处理
8.归并排序
将一个序列分成两个长度相等的子序列,为每一个子序列排序,然后再将它们合并成一个序列。合并两个子序列的过程称为归并
代码
1 | template<class Elem> |
2 | void mergesortcore(Elem A[], Elem temp[], int i, int j) |
3 | { |
4 | if(i == j) return; |
5 | int mid = (i + j)/2; |
6 | |
7 | mergesortcore(A, temp, i, mid); |
8 | mergesortcore(A, temp, mid+1, j); |
9 | |
10 | // 归并 |
11 | int i1 = i, i2 = mid + 1, curr = i; |
12 | while(i1<=mid && i2<=j){ |
13 | if(A[i1] < A[i2]) |
14 | temp[curr++] = A[i1++]; |
15 | else |
16 | temp[curr++] = A[i2++]; |
17 | } |
18 | while(i1 <= mid) |
19 | temp[curr++] = A[i1++]; |
20 | while(i2 <= j) |
21 | temp[curr++] = A[i2++]; |
22 | for(curr = i;curr <= j;curr++) |
23 | A[curr] = temp[curr]; |
24 | } |
25 | |
26 | template<class Elem> |
27 | void mergesort(Elem A[], int sz) |
28 | { |
29 | Elem *temp = new Elem[sz](); |
30 | int i = 0, j = sz - 1; |
31 | mergesortcore(A, temp, i, j); |
32 | delete [] temp; |
33 | } |
性能
- 最佳:时间复杂度为O(nlogn)
- 最差:时间复杂度为O(nlogn)
- 平均:时间复杂度为O(nlogn)
- 辅助空间:O(n)
- 稳定性:稳定
优化
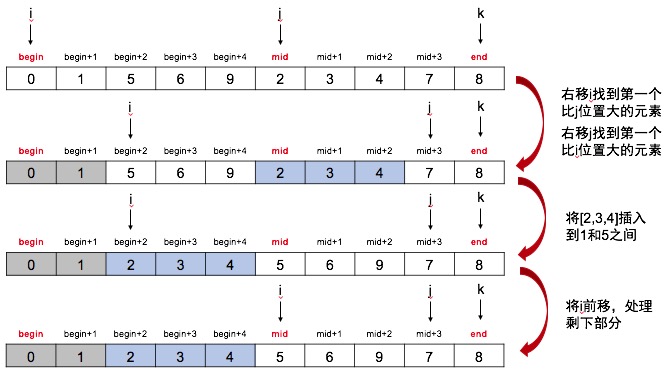
原地归并排序不需要辅助数组即可归并
1 | void reverse(int *arr, int n) |
2 | { |
3 | int i = 0, j = n - 1; |
4 | while(i < j) |
5 | swap(arr[i++], arr[j--]); |
6 | } |
7 | |
8 | void exchange(int *arr, int sz, int left) |
9 | { |
10 | reverse(arr, left); // 翻转左边部分 |
11 | reverse(arr + left, sz - left); // 翻转右边部分 |
12 | reverse(arr, sz); // 翻转所有 |
13 | } |
14 | |
15 | void merge(int *arr, int begin, int mid, int end) |
16 | { |
17 | int i = begin, j = mid, k = end; |
18 | while(i<j && j<=k) |
19 | { |
20 | int right = 0; |
21 | while(i<j && arr[i]<=arr[j]) |
22 | ++i; |
23 | while(j<=k && arr[j]<=arr[i]) |
24 | { |
25 | ++j; |
26 | ++right; |
27 | } |
28 | exchange(arr+i, j-i, j-i-right); |
29 | i += right; |
30 | } |
31 | } |
9.堆排序
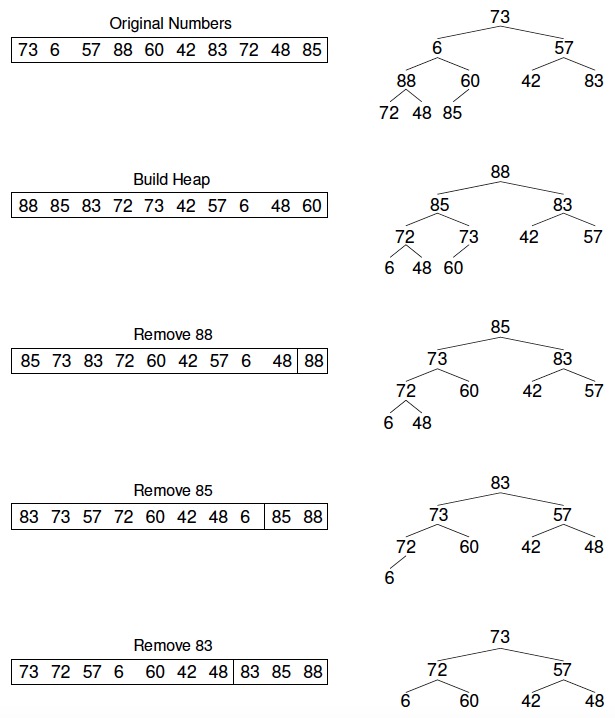
堆排序首先根据数组构建最大堆,然后每次“删除”堆顶元素(将堆顶元素移至末尾)。最后得到的序列就是从小到大排序的序列
代码
这里直接使用C++ STL中堆的构建与删除函数
1 | template <class Elem> |
2 | void heapsort(Elem A[], int n) |
3 | { |
4 | Elem mval; |
5 | int end = n; |
6 | make_heap(A, A+end); |
7 | for(int i=0; i<n; i++) |
8 | { |
9 | pop_heap(A, A+end); |
10 | end--; |
11 | } |
12 | } |
如果不能使用现成的库函数:实现1
1 | /******************************************** |
2 | * 向堆中插入元素 |
3 | * hole:新元素所在的位置 |
4 | ********************************************/ |
5 | template <class value> |
6 | void _push_heap(vector<value> &arr,int hole){ |
7 | value v = arr[hole];//取出新元素,从而产生一个空洞 |
8 | int parent = (hole - 1) / 2; |
9 | //建最大堆,如果建最小堆换成 arr[parent] > value |
10 | while(hole > 0 && arr[parent] < v){ |
11 | arr[hole] = arr[parent]; |
12 | hole = parent; |
13 | parent = (hole - 1) / 2; |
14 | } |
15 | arr[hole] = v; |
16 | } |
17 | |
18 | /******************************************** |
19 | * 删除堆顶元素 |
20 | ********************************************/ |
21 | template <class value> |
22 | void _pop_heap(vector<value> &arr,int sz) |
23 | { |
24 | value v = arr[sz - 1]; |
25 | arr[sz - 1] = arr[0]; |
26 | --sz; |
27 | int hole = 0; |
28 | int child = 2 * (hole + 1); //右孩子 |
29 | while(child < sz){ |
30 | if(arr[child] < arr[child - 1]) |
31 | --child; |
32 | arr[hole] = arr[child]; |
33 | hole = child; |
34 | child = 2 * (hole + 1); |
35 | } |
36 | if(child == sz){ |
37 | arr[hole] = arr[child - 1]; |
38 | hole = child - 1; |
39 | } |
40 | arr[hole] = v; |
41 | _push_heap(arr,hole); |
42 | } |
43 | |
44 | /******************************************** |
45 | * 建堆 |
46 | * sz:删除堆顶元素后的大小 |
47 | * v: 被堆顶元素占据的位置原来的元素的值 |
48 | ********************************************/ |
49 | template <class value> |
50 | void _make_heap(vector<value> &arr) |
51 | { |
52 | int sz = arr.size(); |
53 | int parent = (sz - 2) / 2; |
54 | while(parent >= 0){ |
55 | int hole = parent; |
56 | int child = 2 * (hole + 1); //右孩子 |
57 | value v = arr[hole]; |
58 | while(child < sz){ |
59 | if(arr[child] < arr[child - 1]) |
60 | --child; |
61 | arr[hole] = arr[child]; |
62 | hole = child; |
63 | child = 2 * (hole + 1); |
64 | } |
65 | if(child == sz){ |
66 | arr[hole] = arr[child - 1]; |
67 | hole = child - 1; |
68 | } |
69 | arr[hole] = v; |
70 | _push_heap(arr,hole); |
71 | --parent; |
72 | } |
73 | } |
74 | |
75 | template <class value> |
76 | void heap_sort(vector<value> &arr) |
77 | { |
78 | _make_heap(arr); |
79 | for(int sz = arr.size();sz > 1;sz--) |
80 | _pop_heap(arr,sz); |
81 | } |
如果不能使用现成的库函数:实现2
1 | void Heapify(int A[], int i, int size) // 从A[i]向下进行堆调整 |
2 | { |
3 | int left_child = 2 * i + 1; // 左孩子索引 |
4 | int right_child = 2 * i + 2; // 右孩子索引 |
5 | int max = i; // 选出当前结点与其左右孩子三者之中的最大值 |
6 | if (left_child < size && A[left_child] > A[max]) |
7 | max = left_child; |
8 | if (right_child < size && A[right_child] > A[max]) |
9 | max = right_child; |
10 | if (max != i) |
11 | { |
12 | Swap(A, i, max); // 把当前结点和它的最大(直接)子节点进行交换 |
13 | Heapify(A, max, size); // 递归调用,继续从当前结点向下进行堆调整 |
14 | } |
15 | } |
16 | int BuildHeap(int A[], int n) // 建堆,时间复杂度O(n) |
17 | { |
18 | int heap_size = n; |
19 | for (int i = heap_size / 2 - 1; i >= 0; i--) // 从每一个非叶结点开始向下进行堆调整 |
20 | Heapify(A, i, heap_size); |
21 | return heap_size; |
22 | } |
23 | void HeapSort(int A[], int n) |
24 | { |
25 | int heap_size = BuildHeap(A, n); // 建立一个最大堆 |
26 | while (heap_size > 1) // 堆(无序区)元素个数大于1,未完成排序 |
27 | { |
28 | // 将堆顶元素与堆的最后一个元素互换,并从堆中去掉最后一个元素 |
29 | // 此处交换操作很有可能把后面元素的稳定性打乱,所以堆排序是不稳定的排序算法 |
30 | Swap(A, 0, --heap_size); |
31 | Heapify(A, 0, heap_size); // 从新的堆顶元素开始向下进行堆调整,时间复杂度O(logn) |
32 | } |
33 | } |
性能
根据已有数组构建堆需要O(n)的时间复杂度,每次删除堆顶元素需要O(logn)的时间复杂度,所以总的时间开销为,O(n+nlogn),平均时间复杂度为O(nlogn)
- 最佳:时间复杂度为O(nlogn)
- 最差:时间复杂度为O(nlogn)
- 平均:时间复杂度为O(nlogn)
- 辅助空间:O(1)
- 稳定性:不稳定
注意根据已有元素建堆是很快的,如果希望找到数组中第k大的元素,可以用O(n+klogn)的时间,如果k很小,时间开销接近O(n)
10.桶排序
代码
1 | int PutAt(int n, int max, int k){ // 返回数字n应该放入的桶编号 |
2 | int i = 0; |
3 | while(i < k-1){ |
4 | if(n>max*i/k && n<max*(i+1)/k) // 将0~max划分成k个区间/桶 |
5 | return i; |
6 | i++; |
7 | } |
8 | return i; |
9 | } |
10 | void InsertSort(vector<int>& v){ // 桶内插入排序 |
11 | int temp; |
12 | for(int i=1; i<v.size(); i++) { |
13 | temp = v[i]; |
14 | int j = i - 1; |
15 | while(j>0 && temp<v[j]) { |
16 | v[j + 1] = v[j]; |
17 | j--; |
18 | } |
19 | v[j+1] = temp; |
20 | } |
21 | } |
22 | void BucketSort(vector<int> &v, int max, int k) { // max为数字最大值 |
23 | vector<vector<int> > bucket; |
24 | bucket.resize(k); // 默认k个桶 |
25 | for(int i=0; i<v.size(); i++) |
26 | bucket[PutAt(v[i], max, k)].push_back(v[i]); //入桶 |
27 | for(int j=0; j<bucket.size(); j++) |
28 | // sort(bucket[j].begin(), bucket[j].end()); //快速排序 |
29 | InsertSort(bucket[j]); //插入排序 |
30 | int n = 0; |
31 | for(int i=0; i<bucket.size(); i++) |
32 | for(int j=0; j<bucket[i].size(); j++) |
33 | v[n++] = bucket[i][j]; |
34 | } |
11.基数排序
代码
1 | void RadixSort(int A[], int k, int n) { // 待排序数组,数字位数,数字个数 |
2 | int count = k + 1, bit; |
3 | data *p, *first, *L = new data[10]; // L是以数字0-9为基础的十个数表 |
4 | for(int i=0; i<10; i++) |
5 | L[i].link = 0; |
6 | while(k--) { |
7 | for(int i=0,v; i<n; i++) { // 将当前位数字值相同的数放入相应的表中 |
8 | p = new data; |
9 | p->number = A[i]; |
10 | p->link = 0; |
11 | bit = count - k; //从个位(bit=1)开始的位数号 |
12 | while(bit--) { |
13 | v = A[i] % 10; |
14 | A[i] = A[i] / 10; |
15 | } |
16 | if(L[v].link == 0) |
17 | L[v].link = p; |
18 | else { |
19 | first = L[v].link; |
20 | while(first->link) |
21 | first = first->link; |
22 | first->link = p; |
23 | } |
24 | } |
25 | for(int i=0,v=0; i<10; i++) { // 所有表的数字从小到大从新组织成序列 |
26 | p = L + i; |
27 | first = L[i].link; |
28 | while(first) { |
29 | A[v] = first->number; |
30 | v++; |
31 | p = first; |
32 | first = first->link; |
33 | delete p; |
34 | } |
35 | L[i].link = 0; |
36 | } |
37 | } |
38 | delete []L; |
39 | } |
12.多路归并
多路归并是外部排序最常用的算法:将原文件分解成多个能够一次性装入内存的部分,分别把每一部分调入内存完成排序。然后,对已经排序的子文件进行归并排序
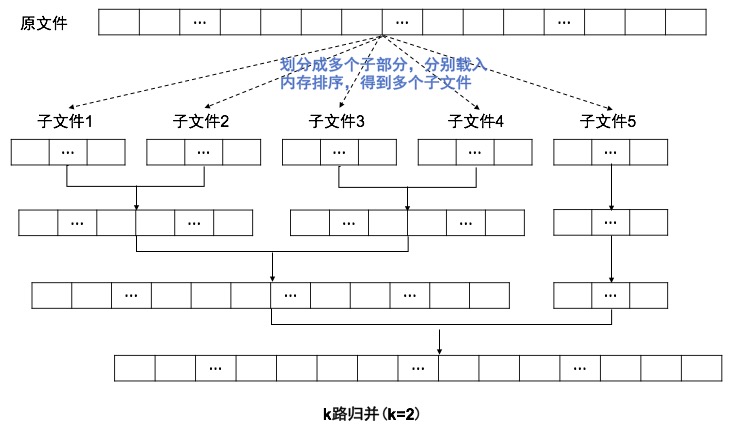
k的选择
假设总共m个子文件,每次归并k个子文件,那么一共需要归并$$\log _{k} m$$次(扫描磁盘),在k个元素中找出最小值(或最大值)需要比较k-1次。如果总记录数为N,所以时间复杂度就是$$(k-1) N \log _{k} m=\frac{(k-1)}{\log k} N \log m$$, 由于 $$\frac{(k-1)}{\log k}$$随k的增大而增大,所以比较次数的增加会逐步抵消“低扫描次数”带来的性能增益,所以对于k值的选择,主要涉及两个问题:
- 每一轮归并会将结果写回到磁盘,那么k越小,磁盘与内存之间数据的传输就会越多,增大k可以较少扫描次数
- k个元素中选取最小的元素需要比较k-1次,如果k越大,比较的次数就会越大
优化
可以利用下列方法减少比较次数:
- 败者树
- 建堆:使用一个k个元素的数组,第一次将k个文件中最小的元素读入数组(并且记录每个元素来自哪个文件),然后建最小堆,将堆顶元素删除,并从堆顶元素的源文件中取出下一个数,插入堆中,调整后重复上述操作。虽然第一次需要遍历k个文件取出最小元素,加上建堆需要一定时间,但是后续操作可以很快完成
