NICE: Non-liner Independent Components Estimation

Paper：https://arxiv.org/abs/1410.8516

导读：本文标题“Non-liner Independent Components Estimation”，即“非线性独立分量估计”，所提模型NICE是一种生成模型，用以对复杂的高维分布建模。生成模型是对数据的概率密度建模，而这一般比较困难。本文的核心思路为：学习一个确定的非线性变换，将数据映射到隐空间，得到独立的隐变量，该过程可逆，即NICE亦可将隐变量从隐空间映射到原始高维数据。

背景问题

• 什么是一个好的分布？其数据分布对于模型来说是简单易处理的，即其数据分布易于建模。
• 非监督学习的一个中心问题是怎样对结构未知的复杂数据分布建模。

本文思想

• 让学习器找一种变换h=f(x)，将数据变换到一个新空间，使得h服从简单的分布pH(h)，比如高斯分布或者均匀分布，由于函数f可逆，我们可以通过对分布pH(h)进行采样得到h，再由x=f^-1(h)对x进行生成。通常h的每个分量hd独立且满足因式分解，即：
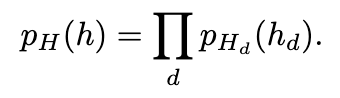
• 选择可逆的变换函数h=f(x)，最终对原始数据建模为：
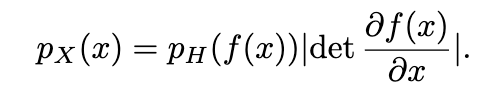
• 对上式作推导如下：
• 至此，生成原始数据x就很容易了：
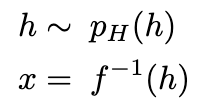
• 对上式作解释如下：数据x的分布可以通过pH(h)和f(x)得到，其中pH(h)由我们自己选取（满足因式分解特性，常常从标准分布族中选取，如高斯分布）；对于f(x)，则需要通过建模学习得到，使其自身可逆且雅可比行列式易计算。

模型构建

• 通过最大似然函数提出学习的映射函数为：

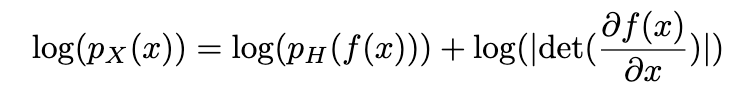
• h满足因式分解且hd独立，得到：

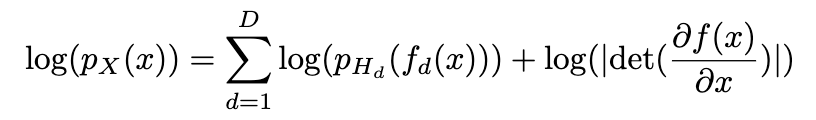
• 允许重新调节（尺度变换层），最终得到：

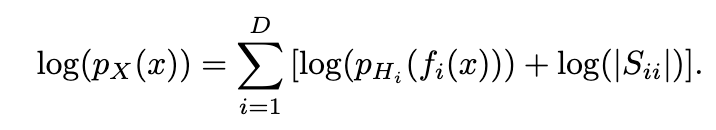
• 解释尺度变换层：当完成模型训练时，可以得到一个生成模型和一个编码模型，但此时随机变量z（隐变量）与x是同尺度的，x虽然是D维的，但未必遍布整个D维空间，存在“维度浪费”情况，故需要S作尺度变换。

• 尺度变化操作：

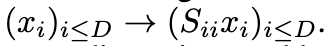
• 解释尺度变换操作：对需要的维度，给予更大的权重；对不需要的维度，给予更小的权重。S可以识别各维度的重要程度，S越小说明该维度越重要，当S很大趋于无穷时，该维度不需要，整个样本数据维度减一。

模型结构与试验结果

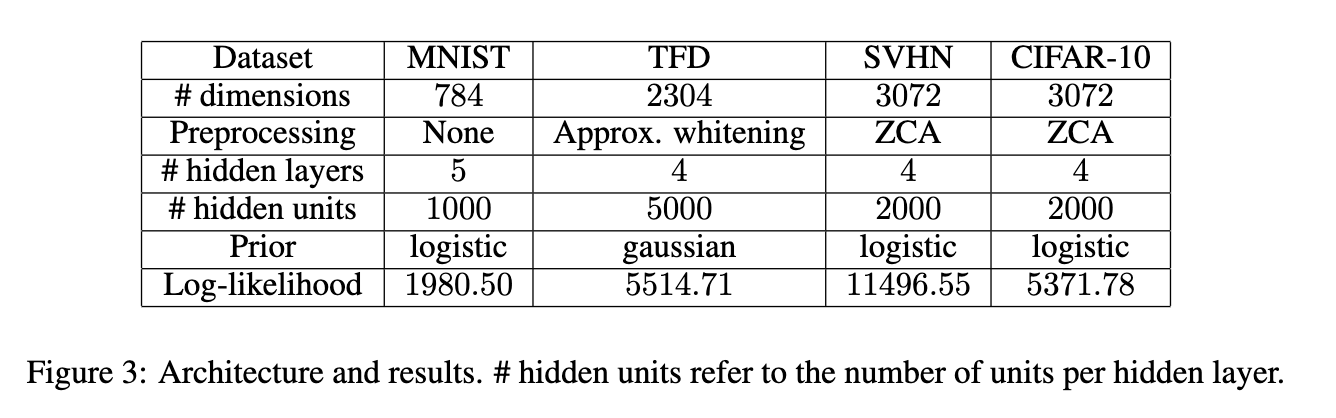
总结

• 本文所提模型NICE为流模型基础，在此基础上逐渐发展出Real NVP模型和Glow模型。
  • 相比VAE（变分自编码器），NICE直接计算似然函数。
  • 相比GAN（生成对抗网络），NICE对潜在变量进行了推断，更有利用的空间。